
이번 시간의 목차
1. 인간을 이긴 컴퓨터 프로그램, 기계학습
2. 기계학습 기법에는 무엇이 있을까?
3. 지도학습: 문제와 정답을 통해 학습시키자
4. 선형회귀 분석에 대해 자세하게 알아보자!
5. 파이썬에서는 어떻게 선형회귀 분석을 하는 걸까?
6. 좀 더 큰 데이터를 다뤄 볼까?
7. 체질량 지수와 당뇨 수치의 관계를 선형회귀로 알아보자!
8. k-NN 알고리즘 분류법이란?
9. k-NN 알고리즘 분류: 붓꽃의 종류 구분
10. k-NN 알고리즘 분류: 분류기의 정확성 확인
11. 사례 분석: 선형회귀로 기대수명 예측하기
12. 상관 관계를 찾고 선형회귀로 나타내자!
13. 마무리
자, 가자! 파이썬의 세계로!
인간을 이긴 컴퓨터 프로그램, 기계학습

2016년, 세상을 한 번 크게 들썩인 사건을 기억하고 있을 것이다. 바로 구글 딥마인드의 알파고(AlphaGo)가 세계 최상위급 프로 기사인 이세돌 9단과의 바둑 경기에서 4승 1패로 승리한 사건이다. 이 경기가 중계된 뒤로 사람들은 컴퓨터(인공지능)가 우리를 지배하게 될 수도 있다며 공포에 찬 목소리를 내거나, '컴퓨터는 플러그를 뽑으면 그만이다'라는 농담을 던지기도 했다.
이 알파고는 컴퓨터에게 바둑 경기의 규칙과 이전 경기의 기보를 알려준 뒤 컴퓨터가 스스로 바둑의 원리를 학습하여 바둑 경기를 진행한 것이다. 이렇게 컴퓨터가 데이터를 기반으로 스스로 학습한다면 컴퓨터는 더욱 더 복잡한 일을 할 수 있을 것이다.
기계학습(Machine Learning)은 인공 지능의 한 분야로, 컴퓨터에 학습 기능을 부여하기 위한 연구 분야이다. 기계학습이라는 용어는 1959년에 아서 사무엘(Arthur Samuel)에 의해 만들어졌다. 패턴 인식 및 계산 학습 이론에서 진화한 기계학습은 주어진 데이터를 보고 컴퓨터가 판단 방법을 학습하게 한다. 이 데이터가 많으면 많을수록 판단을 내리는 알고리즘 성능이 향상된다.
학습 알고리즘은 항상 정해진 동작을 수행하는 명령어로 구성된 알고리즘과는 달리 데이터를 이용하여 예측하고 판단할 수 있게 된다. 기계학습은 주로 스팸 메일 필터링, 네트워크 침입자 자동 검출, 광학 문자 인식, 컴퓨터 비전, 자율주행 등의 분야에서 쓰인다.
기계학습 기법에는 무엇이 있을까?

기계학습은 일반적으로 가르쳐주는 "교사"의 존재 여부에 따라 크게 지도학습과 자율학습으로 나누어지고, 보상과 처벌에 따른 학습을 하는 강화학습으로 분류할 수 있다.
지도학습(Supervised Learning)

컴퓨터가 교사에 의해 주어진 예제와 정답(혹은 레이블)을 제공받는다. 지도학습의 목표는 입력을 출력에 매핑하는 일반적인 규칙을 학습하는 것이다. 예를 들어서 강아지와 고양이를 구분하는 문제라면 강아지와 고양이에 대한 이미지 데이터를 제공한 후에 교사가 어떤 데이터가 강아지인지, 어떤 데이터가 고양이인지를 알려주는 것이다.
자율학습(Unsupervised Learning)

외부에서 정답(레이블)이 주어지지 않고 학습 알고리즘이 스스로 입력에서 어떤 구조를 발견하는 학습이다. 흔히 비지도 학습이라고도 부르는 자율학습을 사용하면 데이터에서 숨겨진 패턴을 발견할 수도 있다. 대표적인 자율학습으로는 클러스터링(Clustering)이 있다. 위처럼 여러 개의 큰 그룹으로 나누어지는 데이터를 보고 스스로 학습하는 것이다. 비슷한 내용을 다루는 인터넷 뉴스 기사를 자동으로 그룹핑하는 것이 예시라고 할 수 있다.
강화학습(Reinforcement Learning)
강화학습은 보상 및 처벌의 형태로 학습 데이터가 주어진다. 주로 차량 운전이나 상대방과의 경기 같은 동적인 환경에서 프로그램의 행동에 대한 피드백만 제공되는 경우이다. 예를 들어서 바둑에서 어떤 수를 두고 승리했다면 보상이 주어지는 방식이라 할 수 있다.
지도학습: 문제와 정답을 통해 학습시키자
지도학습은 주어진 입력-출력(x-y) 쌍을 통해 학습한 후에 새 입력값을 보고 합리적인 출력값을 예측하는 것이다. 지도학습의 목적이 입력 x에 대한 출력 y의 매핑함수 f( )를 학습하는 것이라 할 수도 있다.

예를 들어 좌표평면 위의 점 (x, y)에 대해 (1, 1), (2, 2), (3, 3), (4, 4)가 주어진다고 하자. 컴퓨터는 x와 y의 관계를 y = x라고 표현할 수 있다는 것을 모르는 상태이고, 네 점으로 학습한 뒤에 x = 5를 입력하면 y값이 5라는 답변을 받아내는 것이 목표가 되는 것이다.
이 문제는 지도학습 중에서도 회귀분석(Regression)을 통해 해결할 수 있다. 회귀는 일반적으로 데이터들을 다차원 공간에 표시한 후에 이 데이터를 가장 잘 설명하는 직선이나 곡선을 찾는 문제라고 생각할 수 있따. 회귀분석은 연속적인 값을 예측한다. 위의 예시 그래프처럼 y = f(x)에서의 입력 x와 출력 y를 보면서 함수 f(x)를 예측하는 것이다.

전통적인 선형회귀(Linear Regression)는 기계학습이라기엔 너무 단순하고, 기계학습보다는 통계에 가깝다고 생각하는 사람들이 많다. 하지만 이 역시도 f( )라는 매핑 함수를 학습하는 것이므로 기계학습이라 할 수 있다.
데이터를 학습시킬 때 데이터를 원형 그대로 사용할 수도 있지만, 일반적으로는 데이터에서 어떤 특징(Features)을 추출해서 이 특징을 학습시키고 테스트한다. 이때 특징은 관찰한 현상에서 측정할 수 있는 개별적인 속성을 의미한다. 이메일이 스팸인지 아닌지를 걸러내는 것을 예로 들자면 '로또', '광고' 등의 문자열을 포함한다거나, 제목이나 본문에 '★' 같은 특수문자를 포함하는 등이 특징이 될 수 있다.
선형회귀 분석에 대해 자세히 알아보자!
선형회귀는 임의의 변수 x와 이 변수에 따른 또 다른 변수 y와의 상관관계를 모델링하는 기법이다. 이 두 변수의 관계를 알아내거나 이를 이용하여 y가 밝혀지지 않은 x값에 대해 y를 예측하는 데에 사용할 수 있다. 우선 가장 간단한 선형 모델을 살펴보자.
|
y = mx + b
# m은 직선의 기울기(계수)
# b는 y절편
|
cs |
바로 일차함수이다. m은 기울기로, 입력 변수 x에 곱해지는 계수(Coefficient)이고, b는 절편(intercept)이다. 기본적으로 선형회귀 알고리즘은 데이터를 설명하는 가장 적절한 기울기와 절편값을 찾는다. x변수는 데이터의 특징이라 바꿀 수 없고, 우리는 이 m과 b를 제어할 수 있다. 선형회귀 알고리즘은 기본적으로 데이터 요소에 여러 직선을 갖다 대 보고 가장 작은 오류를 내는 직선을 반환한다.
이 개념은 2개 이상의 변수가 있는 경우까지 확장할 수 있다. 이때는 다중회귀 분석이라고 한다. 예를 들어 주택의 면적, 침실 수, 해당 지역 사람들의 평균 소득, 주택의 노후화 등을 기준으로 주택 가격을 예측해야 하는 경우가 있다고 해 보자. 이 경우 종속 변수 y는 여러 독립 변수에 종속되고, p개의 변수가 포함된 회귀 모델은 아래와 같이 나타낼 수 있다.
|
y(w, x) = w0 + w1x1 + w2x2 + ... + wpxp
# w, x : 벡터
# w1~2p : 계수
# w0 : 절편
|
cs |
이때 w와 x는 모두 벡터이고 w1에서 wp까지를 계수(Coefficient), w0를 절편(intercept)라 한다. 이 식은 평면의 방정식이고, 3차원에서 나타낼 수 있다. 아까 살펴본 일차함수는 2차원 공간에서 나타낼 수 있다. 3차원 이상으로 가면 초평면(Hyperplane)이라 한다.
파이썬에서는 어떻게 선형회귀 분석을 하는 걸까?
파이썬에서 가장 많이 사용되는 기계학습 라이브러리 중에는 사이킷런(Scikit-Learn)이라는 것이 있다. 이 사이킷런은 파이썬 언어에서 기계학습을 수행하는 라이브러리로, 선형회귀, k-NN 알고리즘, 서포트 벡터머신, 랜덤 포레스트, 그래디언트 부스팅, k-means 등의 분류, 회귀, 클러스터링 알고리즘을 포함하고 있어서 기계학습을 처음 접하는 사람들에게 유용한 도구로 자리잡고 있다.
앞에서 선형회귀에 대해 알아보았으니, 이제 선형회귀 분석을 실제로 해보자.
우선 본격적으로 시작하기 전에 사이킷런을 코드에 가져와야 한다. 사이킷런은 sklearn이라는 이름으로 불러올 수 있다.
|
import numpy as np
from sklearn import linear_model #scikit-learn 모듈을 가져옴.
regr = linear_model.LinearRegression() #선형회귀 모델 생성
|
cs |
이렇게 사이킷런(sklearn)에서 선형회귀(linear_model)을 불러왔다. 아래에 있는 regr는 LinearRegression()이라는 함수를 통해 선형회귀 모델을 생성하고 regr라는 변수에 담은 것이다.
이제 진짜로 시작해보자.
반에 있는 4명의 학생을 임의로 추출하여 키와 몸무게를 측정하고, 키가 169 cm인 학생의 몸무게를 예측해 볼 것이다.
|
# sklearn은 벡터값을 대문자로 표현해서 x보다는 X로 쓰는 것이 적합하다.
X = [[164], [179], [162], [170]]] #다중회귀에 적용되도록 함
y = [53, 63, 55, 59] #y = f(X)의 결과
regr.fit(X, y) #선형회귀 에 X, y를 적용한다.
|
cs |
X에 키 데이터를 2차원 리스트로 넣고, y에 몸무게를 리스트로 초기화시킨다. 이때 학습 데이터는 여러 변수에 대해서 다중회귀 분석을 실시하기 위해 반드시 2차원 배열로 되어야 한다. X가 다수의 종속 변수를 포함하는 벡터임을 꼭 기억해야 한다. 항목이 하나 밖에 없어도 [164]같은 배열 형태로 만들어야 한다.

이렇게 fit(X, y)를 통해 만들어진 모델은 y = w0 + w1X1 처럼 표시할 수 있다. 여기서 기울기는 w1이고, 절편은 w0이 된다. 이 선형회귀 모델이 기울기와 절편을 어떻게 만들었는지와 얼마나 잘 예측했는지는 아래처럼 확인할 수 있다.
|
>>> coef = regr.coef_ #직선의 기울기
>>> intercept = regr.intercept_ #직선의 절편
>>> score = regr.score(X, y) #예측을 얼마나 잘 했나
>>> print("y = ", coef, '* X + ', intercept)
y = [0.55221745] * X + -35.68669527896999
>>> print("The score of this line for the data: ", score)
The score of this line for the data: 0.903203123105648
|
cs |
각각 coef_, intercept_ 특성값과 score(X, y) 함수를 사용했다. 선형관계에 가까운 데이터를 사용했기 때문에 score(X, y)의 반환값으로는 1에 가까운 값을 얻을 수 있다.
이제 이 데이터를 바탕으로 새 입력이 주어졌을 때의 결과를 예측해야 한다. 이 예측은 우리가 학습을 통해 찾아 놓은 직선의 방정식을 통해 이루어질 것이다. 컴퓨터는 백지 상태에서 위의 데이터를 학습하고 새로 들어올 데이터도 이전 데이터와 같은 방식의 관계를 가질 것이라 예측한다.
|
>>> input_data = [[180], [185]] #새로 예측해 볼 데이터
>>> result = regr.predict(input_data) #결과 예측은 predict()로!
>>> print(result)
[63.71244635 66.47353362] #약 63 kg, 66 kg로 예상한다.
|
cs |
예측까지 끝났다면 이제 선형회귀를 그래프로 그려보자. 앞에서 다룬 맷플롯립 라이브러리를 활용하면 쉽게 그릴 수 있다!
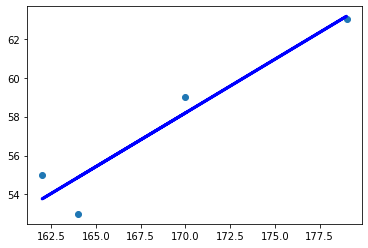
|
import numpy as np
from sklearn import linear_model #scikit-learn 모듈을 가져옴.
import matplotlib.pyplot as plt
regr = linear_model.LinearRegression() #선형회귀 모델 생성
# sklearn은 벡터값을 대문자로 표현해서 x보다는 X로 쓰는 것이 적합하다.
X = [[164], [179], [162], [170]] #다중회귀에 적용되도록 함
y = [53, 63, 55, 59] #y = f(X)의 결과
regr.fit(X, y)
#(X, y)의 점을 찍는다.
plt.scatter(X, y)
#y 예측값을 계산한다.
y_pred = regr.predict(X)
#학습 데이터와 예측값으로 선 그래프를 그림.
#계산된 기울기와 y절편을 갖는다.
plt.plot(X, y_pred, color = 'blue', linewidth = 3)
plt.show()
|
cs |
좀 더 큰 데이터를 다뤄 볼까?
앞에서 다룬 선형회귀는 사람의 키를 추정하기 위해서 소수의 특징만을 고려했지만, 이제는 더 많은 정보와 더 많은 특징을 가진 더 복잡한 데이터를 다뤄 보자.
이번 시간에는 sklearn 라이브러리에서 제공하는 당뇨병 환자들의 데이터를 사용할 것이다.
|
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn import datasets #sklearn에서 datasets를 가져온다.
#당뇨병 데이터 세트를 sklearn의 데이터집합에서 가져온다.
diabetes = datasets.load_diabetes()
|
cs |
데이터를 가져오려면 우선 사이킷런에서 데이터집합(datasets)를 불러와야 한다. 그런 다음 load_diabetes() 함수를 통해 diabetes라는 변수에 해당 데이터를 모두 저장한다.
|
print('shape of diabetes.data: ', diabetes.data.shape)
print(diabetes.data)
print('입력 데이터의 특성들: ', diabetes.feature_names)
print('target data y: ', diabetes.target.shape)
-------------------------------------
shape of diabetes.data: (442, 10) # 442행(데이터) 10개의 특징.
[[ 0.03807591 0.05068012 0.06169621 ... -0.00259226 0.01990842
-0.01764613]
[-0.00188202 -0.04464164 -0.05147406 ... -0.03949338 -0.06832974
-0.09220405]
[ 0.08529891 0.05068012 0.04445121 ... -0.00259226 0.00286377
-0.02593034]
...
입력 데이터의 특성들: ['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3',
's4', 's5', 's6']
target data y: (442,) #데이터가 442개이므로 스칼라도 442.
|
cs |
shape는 데이터 세트의 형태를 출력한다. (442, 10)을 반환하므로 442 * 10형태를 띠고 있고, 442는 행의 개수이며, 10은 데이터 세트의 특징 개수를 의미한다. 이 10개의 특성을 feature_names 로 확인할 수 있다. 나이, 성별, bmi, 혈압, s1부터 s6(당뇨 수치에 영향을 주는 각종 검사값)이 있다. 입력에 따라 얻어야 하는 출력값(타겟)은 target에 저장된다. 총 442개의 데이터를 가지기 때문에 출력은 442의 스칼라 값이 된다.
diabetes.data를 출력해봤을 때 보이듯이 이번 데이터는 수도 많고 특징도 늘어났기 때문에 sklearn의 선형회귀 모델은 훨씬 복잡해지고, 선형회귀 모델 말고 다른 기계학습 알고리즘을 적용할 수도 있다.
체질량 지수와 당뇨 수치의 관계를 선형회귀로 알아보자!
당뇨병 데이터에 대해 알아보았으니 이제 진짜로 선형회귀 분석을 시작해보자.
분석을 시작할 때 가장 먼저 해야 할 것은 가설 세우기이다. 데이터의 10가지 특징들 중에서도 당뇨 수치에 밀접한 영향을 주는 특징이 있을 수 있다. 그러므로 이번 시간에서의 가설은 《체질량 지수가 높은 사람은 당뇨 수치가 높을 가능성이 있다.》 로 정하자.
그렇다면 우리에게 필요한 항목은 무엇일까? 체질량 지수가 높은 사람을 기준으로 잡았으니, 체질량 지수인 BMI값이 필요할 것이다. 나머지 항목에 대한 데이터는 지금은 쓰지 않을 것이니 BMI 값만 따로 떼어 내 보자.
|
X = diabetes.data[:, 2]
print(X) #(442,)형태의 배열 출력
-------------------------------
[ 0.06169621 -0.05147406 0.04445121 -0.01159501 -0.03638469 -0.04069594
-0.04716281 -0.00189471 0.06169621 0.03906215 -0.08380842 0.01750591
-0.02884001 -0.00189471 -0.02560657 -0.01806189 0.04229559 0.01211685
...
|
cs |
그냥 평소에 리스트나 넘파이배열, 데이터 프레임을 슬라이싱 하듯이 슬라이싱하면 된다. 하지만 조금 전에 말했듯이 입력값 X는 2차원 배열이어야 한다. 따라서 위처럼 슬라이싱된 날것의 1차원 배열은 선형회귀의 입력 데이터로 쓸 수 없다. 그래서 한 번 더 가공을 거쳐야 한다.
이때는 넘파이의 newaxis 속성을 이용한다.
|
X = diabetes.data[:, np.newaxis, 2] #배열의 차원을 증가시킨다.
print(X)
-------------------------------
[[ 0.06169621]
[-0.05147406]
[ 0.04445121]
[-0.01159501]
[-0.03638469]
[-0.04069594]
[-0.04716281]
... #2차원으로 바뀌었다!
|
cs |
np.newaxis는 현재 배열의 차원을 1 증가시키는 역할을 한다. 위에서는 1차원 배열에 newaxis를 적용했으므로 2차원 배열로 바뀌는 것을 볼 수 있다.
이제 데이터를 가공하는 것까지 끝냈으니 이 데이터를 선형회귀 모델에 적용해야 하는데... 있는 데이터를 전부 학습용으로 써 버리면 만들어진 모델을 테스트 해 볼 데이터가 없다. 그래서 원래 데이터 중 일부는 학습에 사용하고 일부는 테스트용으로 쓰는 것이 좋다. 실제로 많은 기계학습에서 이런 전략으로 학습의 수준을 평가한다.
|
from sklearn.model_selection import train_test_split #학습 데이터/테스트 데이터 분리
X_train, X_test, y_train, y_test = train_test_split(diabetes.data[:, np.newaxis, 2],
diabetes.target, test_size = 0.2)
regr = LinearRegression()
regr.fit(X_train, y_train)
print(regr.coef_, regr.intercept_)
|
cs |
학습용 데이터와 테스트용 데이터를 분리하려면 sklearn에서 제공하는 train_test_split() 함수를 사용할 수 있다. train_test_split()을 sklearn.model_selection에서 불러오고, 인자로 입력 데이터, 출력 데이터를 넣어주고, 마지막에 테스트에 사용할 데이터의 비율을 넣어준다. 위의 코드에서는 0.2로, 전체의 20%만 사용한다. 분리가 끝났다면 regr.fit(X_train, y_train)으로 선형회귀 모델에 적용시킨다.
|
score_train = regr.score(X_train, y_train) #학습용 학습 결과
score_test = regr.score(X_test, y_test) #테스트용 학습 결과
print(regr.coef_, regr.intercept_) #선형회귀의 기울기와 절편
print('train =', score_train)
print('test =', score_test)
---------------------------
[970.62535212] 151.24354076148921
train = 0.35577351457855644
test = 0.28634341339320646
|
cs |
전체 데이터를 학습시킨 것과 거의 유사한 계수와 절편을 얻는다.
80%만 뽑아서 학습시킨 결과가 얼마나 선형 함수를 잘 따르는지를 확인하려면 20%에 해당하는 테스트용 데이터 선형 함수와 비교하할 수 있다. 학습용은 0.355 정도 선형 함수를 따르는데, 테스트용 데이턴느 0.286 정도가 따른다. 너무 달라도 그렇게 놀랄 건 없다! 컴퓨터는 80%에 해당하는 데이터만 활용했으니 어떻게 보면 당연한 결과다.
지도학습에서 컴퓨터에게 데이터를 주고 학습을 시키고 결과를 예측하게까지 만들었다.
이제 이 컴퓨터가 얼마나 예측을 잘 하는지 알아보아야 한다. 그런데 학습 시에 사용되었던 데이터가 들어온다면 어떤 결과가 나올까? 당연히 좋은 결과를 얻을 것이다. 학습하는 것은 사람과 똑같다. 기출문제를 몇 번이나 돌려 풀고 시험을 치러 가면 문제를 보자마자 풀이과정을 쓰고 답을 쓰듯이, 컴퓨터도 이미 다뤄 본 데이터를 다시 다루면 좋은 결과를 내놓는다. 따라서 한 번도 본 적 없는 '새로운 데이터'로 시스템을 테스트해야 한다.
데이터를 분리하고 모델에 적용까지 시켰으니 이제 이 모델이 얼마나 일반화(Generalization)와 예측을 잘 하는지 알아봐야 한다. 80%를 학습용으로 쓰고 남은 20%의 데이터를 이용하자.
|
X_train, X_test, y_train, y_test = train_test_split(diabetes.data,
diabetes.target, test_size = 0.2)
regr.fit(X_train, y_train) #학습용 데이터를 선형회귀 모델에 적용
y_pred = regr.predict(X_test) #테스트 데이터로 예측한다.
print(y_pred) #예측한 결과
print(y_test) #정답 레이블
---------------------------
[157.45816508 125.70575607 180.63920833 131.30270494 186.62292938
73.48786087 56.53041967 183.44074447 54.16676612 48.62296541
...
[155. 83. 124. 182. 164. 48. 70. 283. 85. 72. 47. 51. 317. 233.
42. 186. 258. 296. 97. 58. 144. 74. 275. 75. 209. 258. 346. 72.
|
cs |
이렇게 수치로만 살피면 어느 정도가 일치하고 어느 정도 오차가 있는지 한눈에 보기 어렵다. 그렇다면 2차원 평면에 y_pred[n]과 y_test[n]을 짝지어서 x, y 라는 원소를 가지는 점으로 출력하면 이 오차를 시각화 할 수 있을 것이다. 그리고 비교를 위해 완벽한 예측 결과를 나타내는 y = x 직선을 함께 출력하자.

|
plt.scatter(y_pred, y_test, color = 'black')
x = np.linspace(0, 330, 100) #특정 구간의 점
plt.plot(x, x, linewidth = 3, color = 'blue')
plt.show()
|
cs |
y = x 직선에 가까울수록 y_pred와 y_test가 서로 일치한다는 뜻이지만, 오차로 인해서 y_pred가 추정한 값이 실제값 y_test와 차이가 나게 된다. 사이킷런에서는 이런 오차값을 구하는 기능을 제공한다. 각각의 예측과 목표값의 차이를 제곱하여 모두 더한 뒤에 전체 데이터의 개수 n으로 나누는 방법인 최소 제곱 오차(Mean Square Error) 이다. 이 오차를 얻기 위해서는 아래처럼 입력해야 한다.
|
#이전 절에서 구한 선형회귀 모델의 코드
from sklearn.metrics import mean_squared_error
regr = LinearRegression()
regr.fit(X_train, y_train)
print('Mean squared error:', mean_squared_error(y_test, y_pred))
-------------------------------------------
Mean squared error: 3173.7323743797933
|
cs |

왼쪽 선형회귀를 살펴보면 점과 선 사이에 거리가 꽤 있는 것을 알 수 있다. 이를 에러(Error)라고 하는데, 이 e1부터 e4까지전체 에러의 합이 0이 되는 모델이 가장 바람직한 모델이자, 우리가 구해야 하는 모델이다. 하지만 왼쪽 그림처럼 직선 거리를 더해버리면 아주 큰 에러가 생겨도 합이 0이 나오는 문제점이 생길 수 있다. 그 문제를 막기 위해 오른쪽처럼 직선에 제곱을 추가하여 에러를 구한다.
k-NN 알고리즘 분류법이란?
지금까지 선형회귀에 대해 알아보았으니, 이번에는 분류하는 방법에 대해 알아보자.

위의 그림을 살펴보면 이 데이터의 특징 공간은 초록 사각형, 빨간 원, 파란 삼각형의 3가지로 나누어져있다. 이렇게 서로 다른 도형들을 클래스(Class)라 하고, 이 클래스가 나타나는 공간이 특징 공간(Feature Space)이라고 부르는 좌표이다. 여기에는 개의 Length와 Height라는 두 가지의 특징이 있기 때문에 2차원 공간에 수평, 수직 방향으로 표시할 수 있지만 3가지 특징이 있음녀 3차원 공간, 그보다 더 많아지면 더 많은 차원의 공간이 필요하다.
위의 데이터를 살피면 산포도 그래프의 왼쪽 하단에는 길이와 높이 모두 짧은 특징을 가지는 말티즈가 분포하고 있고, 오른쪽 하단에는 길이가 길고 높이가 낮은 닥스훈트, 오른쪽 상단에는 길이와 높이 모두 긴 특징을 가지는 사모예드가 분포한다. 이런 특징을 가지는 데이터를 효과적으로 분류하기 위해 우리는 k-NN 알고리즘을 이용한 분류법을 사용한다.
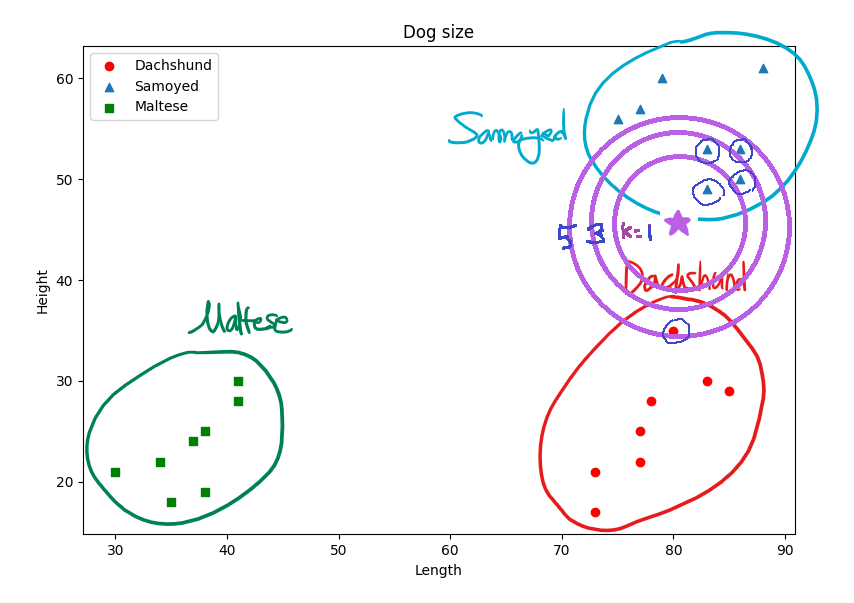
k-NN 방법은 새로운 데이터와 가까운 이웃을 확인하고 가장 많이 나타난 유형을 판단하는 방법이다. 가장 근접한 위치에 있는 이웃에만 의존하기 때문에 최근접 이웃(Nearest Neighbor)이라고도 불린다. 위의 그림을 보면 보라색 별이라는 새로운 데이터가 생겼다. 이 데이터에서 가장 가까이 있는 k개의 데이터를 확인한다.
위의 예시에서 k = 1이면 가장 가까운 데이터 1개를 살피므로, 파란 세모(사모예드)만이 나타난다. 이 경우에 보라색 별은 파란 세모 그룹인 사모예드 클래스에 추가되어야 한다. 하지만 k = 3, k = 5로 늘리다보면 파란 세모뿐만 아니라 빨간 동그라미도 확인된다. 이렇게 k-NN 알고리즘은 k의 값에 따라 결과가 달라진다. 이때 k의 값은 판단의 편의를 위해 일반적으로 홀수를 취한다.
만약 어느 k의 범위에서 두 가지 이상의 클래스 개수가 동일하게 나타난다면 평균적인 거리가 가까운 클래스로 분류하는 것이 합리적이다. 이것을 수학적으로 추가하자면, 거리가 가까운 도형에게 높은 가중치를, 거리가 먼 도형에게 적은 가중치를 가지도록 하고, 그런 다음 모든 도형의 가중치를 합한다. 최종적으로 가장 큰 가중치를 가진 도형의 클래스로 분류하게 된다.
이 k-NN 분류 방법은 특징 공간에 있는 모든 데이터에 대한 정보가 필요하기 때문에 데이터와 클래스가 많이 있으면 메모리 공간과 계산 시간이 많이 필요하다는 단점이 있지만, 알고리즘이 매우 단순해서 직관적이고, 사전 학습이나 특별한 준비 시간이 필요 없다는 장점이 있다.
k-NN 알고리즘 분류: 붓꽃의 종류 구분
k-NN 알고리즘에 대해서 알아보았으니 이제는 실제로 해 볼 차례이다.
sklearn에서는 다양한 데이터 세트를 지원한다. 이번에 사용해 볼 데이터는 붓꽃이다. 붓꽃도 종류가 많이 있지만, 이 사이킷런의 데이터 세트에서 지원하는 150개의 데이터는 총 3종류의 붓꽃으로 나뉜다.
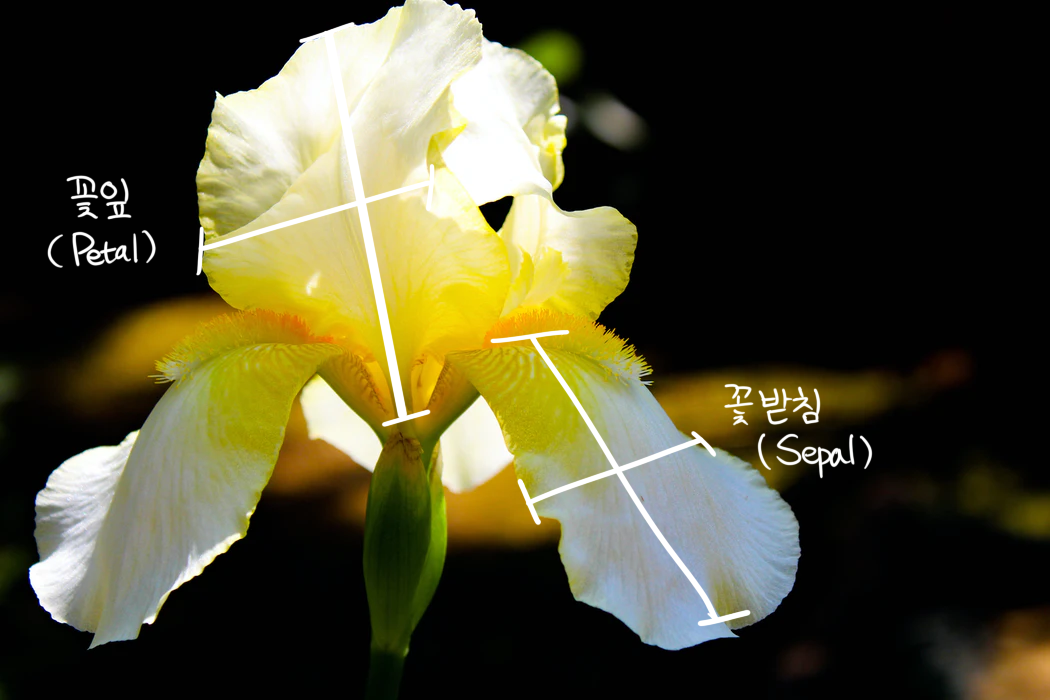
각 데이터는 꽃받침의 길이/너비, 꽃잎의 길이/너비에 대한 정보를 가지고 있으며, 지도학습을 위해 각 데이터마다 붓꽃 종 이름 레이블을 갖고 있다. 종의 이름은 Setosa, Versicolor, Virginica로, 각 종에 따라 꽃받침의 길이와 너비, 꽃잎의 길이와 너비가 약간씩 차이 난다.
우리가 만들 k-NN 알고리즘의 목표는 꽃받침과 꽃잎의 크기를 측정한 데이터를 기반으로 새로운 종을 분류하는 모델이다. 본격적으로 시작하기 전에 사이킷런에서 데이터를 받아 오자.
|
from sklearn.datasets import load_iris
iris = load_iris()
print(iris.data)
--------------------------------
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]
[5.4 3.9 1.7 0.4]
...
|
cs |
이 iris.data를 출력해보면 총 4개의 열을 갖는 150개의 데이터(이는 iris.data.shape로 확인할 수 있다.)를 볼 수 있는데, 이 각각의 열이 4개의 측정값(꽃받침 길이/너비, 꽃잎 길이/너비)을 나타낸다.

iris.data는 위와 같은 형태로 이루어져 있으며, 레이블은 0(Setosa), 1(Versicolor), 2(Virginica)라는 이름으로 저장되어 있다.
|
print(iris.feature_names) #특징의 이름을 출력한다.
print(iris.target) #정답 레이블을 출력한다.
--------------------------------
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
|
cs |
위를 살펴보면 특징의 이름은 꽃받침 길이(Sepal Length)와 너비(Sepal Width), 꽃잎 길이(Petal Length)와 너비(Petal Width)로 이루어져 있고, 단위는 cm임을 알 수 있다. 또, iris.target을 출력해보면 레이블이 0, 1, 2로 인코딩되어 있는 것도 확인할 수 있다. 여기서는 iris.data가 입력이고, iris.target이 학습 레이블이다.
이제 본격적으로 k-NN 분류를 시작해보자.
우선 학습 데이터와 테스트용 데이터를 분리하는 것부터 시작해야 한다.
|
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size = 0.2)
# iris.data와 iris.target을 80:20으로 분리한다.
|
cs |
이렇게 학습용 데이터와 테스트용 데이터를 분리했다면 KNeighborClassifier를 사용하여 학습과 테스트를 진행할 차례다. sklearn의 metrics를 사용하여 accuracy_score() 함수를 불러온다. 이 함수를 쓰면 k-NN의 예측치 y_pred와 실제값 y_test의 차이를 확인할 수 있다.
|
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
num_neigh = 1 # k-NN 의 k값
knn = KNeighborsClassifier(n_neighbors = num_neigh)
knn.fit(X_train, y_train) #학습용 데이터를 학습
y_pred = knn.predict(X_test) #테스트 데이터를 분류시킨다.
scores = metrics.accuracy_score(y_test, y_pred) #정확도
print('n_neighbors가 {0:d}일 때 정확도 {1:.3f}'.format(num_neigh, scores))
--------
n_neighbors가 1일 때 정확도 0.933
|
cs |
위의 코드에서는 k = 1을 사용한다. 이 n_neighbors를 따로 지정해주지 않으면 디폴트값인 k = 5를 따른다. 일반적으로 k의 값이 증가함에 따라 정확도가 증가하지만, 너무 과하게 커질 경우는 정확도가 다시 감소하니 적절하게 k를 정하고 사용해야 한다.
이번에는 학습 데이터와 테스트용 데이터를 나누지 말고 사용 가능한 모든 데이터를 이용해서 학습시켜 보자. n_neighbors 매개변수로는 6을 주고 시작해보자.
|
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
iris = load_iris()
knn = KNeighborsClassifier(n_neighbors = 6)
knn.fit(iris.data, iris.target) #k-NN 분류기 모델 생성
classes = {0: 'setosa', 1:'versicolor', 2: 'virginica'}
#새로운 데이터를 준다.
X = [ [3, 4, 5, 2], [5, 4, 2, 2]]
y = knn.predict(X)
print(classes[y[0]])
print(classes[y[1]])
-----
versicolor
setosa
|
cs |
결과와 같이 k-NN 분류기는 [3, 4, 5, 2] 특성값을 가진 데이터는 vericolor 종으로, [5, 4, 2, 2] 특성을 가지는 데이터는 setosa 종으로 분류한다.
k-NN 알고리즘 분류: 분류기의 정확성 확인
accuracy_score()의 함수로는 어떤 클래스를 어떤 클래스로 오인하는지는 파악하기 어렵다. 각각의 클래스에 속한 데이터가 어떤 클래스로 판별되었는지를 세어서 살피면 더 좋은 관찰을 할 수 있을 것이다.
iris.data의 규모가 적은 편이기도 하니, 전체 데이터에 대한 분류를 실시해보자. iris.data를 분류기에 넣고, 결과 y_pred_all을 구하고 iris.target과 비교해보자.
|
num_neigh = 5
y_pred_all = knn.predict(iris.data)
scores = metrics.accuracy_score(iris.target, y_pred_all)
print('n_neighbors가 {0:d}일때 정확도: {1:.3f}'.format(num_neigh, scores))
-----
n_neighbors가 5일때 정확도: 0.973
|
cs |
위의 정확도 점수를 볼 때, 3%의 오분류가 있음을 확인할 수 있다. (정답, 예측)의 쌍으로 데이터를 만들어 2차원 히스토그램을 그려보면 혼동 행렬을 가시화 할 수 있다.


|
import matplotlib.pyplot as plt
#왼쪽 그래프
plt.hist2d(iris.target, y_pred_all, bins = (3, 3), cmap = plt.cm.jet)
#오른쪽 그래프
plt.hist2d(iris.target, y_pred_all, bins = (3, 3), cmap = plt.cm.gray)
|
cs |
사이킷런에서는 이와 비슷하게 혼동 행렬을 구하는 함수가 있다. 가시화하는 함수 역시 존재한다.



|
from sklearn.metrics import confusion_matrix
conf_mat = confusion_matrix(iris.target, y_pred_all)
print(conf_mat)
plt.matshow(conf_mat)
-------
[[50 0 0]
[ 0 48 2]
[ 0 2 48]]
|
cs |
위의 conf_mat 의 결과를 살펴보면 클래스 1의 데이터 2개가 2로, 클래스 2의 데이터 2개가 1로 잘못 분류된 것을 볼 수 있다.
사례 분석: 선형회귀로 기대수명 예측하기
이제는 공개된 데이터를 바탕으로 예측하는 모델을 만들어 보자. 여기서 사용할 데이터는 캐글(Kaggle) 사이트에서 가져온 것이다. 세계보건기구에서 내어 놓은 각 나라별 기대수명 데이터로 2010년부터 2015년까지 나라별 기대수명과 보건예산, 질병 통계, 비만도 등이 정리되어 있다. 역시 이 책의 github 사이트(https://github.com/dongupak/DataSciPy/blob/master/data/csv/Life_expectancy.csv)에 정리되어 있다.

알파벳 순서대로 국가가 나열되어 있고, 2000년부터 2015년까지의 데이터가 있다. 기대수명은 4번째 열에 나타나 있고, 나라별로 기대수명을 제외하면 20개의 속성이 있는 것을 확인할 수 있다. 이 데이터는 나라별로 집계되지 않은 데이터도 존재해서 결손 데이터가 상당히 존재한다.
데이터가 준비됐다면 이를 파이썬에서 활용할 수 있도록 가공하자. csv 파일을 다루는 데에는 판다스가 유용하다고 이미 저번 시간에 배운 적 있다. 이 csv 파일을 판다스로 읽어오자. 이때 데이터의 시각화를 위한 라이브러리인 Seaborn도 불러온다.
|
import pandas as pd
import seaborn as sns #시각화를 위한 라이브러리, Seaborn
life = pd.read_csv("D:\life_expectancy.csv")
print(life.head())
---------
Country Year ... Income composition of resources Schooling
0 Afghanistan 2015 ... 0.479 10.1
1 Afghanistan 2014 ... 0.476 10.0
2 Afghanistan 2013 ... 0.470 9.9
3 Afghanistan 2012 ... 0.463 9.8
4 Afghanistan 2011 ... 0.454 9.5
[5 rows x 22 columns]
|
cs |
이 데이터에서 우리가 필요한 데이터만 정리해서 따로 빼고 싶으면 데이터프레임을 슬라이싱한다. 열 별로 슬라이싱을 해오려면 필요한 열의 이름을 담은 리스트를 대괄호 속에 넣어준다.
|
life = life[ ['Life expectancy', 'Year', 'Alcohol',
'Percentage expenditure', 'Total expenditure',
'Hepatitis B', 'Measles', 'Polio', 'BMI', 'GDP',
'Thinness 1-19 years', 'Thinness 5-9 years'] ]
print(life)
---------
Life expectancy Year ... Thinness 1-19 years Thinness 5-9 years
0 65.0 2015 ... 17.2 17.3
1 59.9 2014 ... 17.5 17.5
2 59.9 2013 ... 17.7 17.7
3 59.5 2012 ... 17.9 18.0
4 59.2 2011 ... 18.2 18.2
... ... ... ... ... ...
2933 44.3 2004 ... 9.4 9.4
2934 44.5 2003 ... 9.8 9.9
2935 44.8 2002 ... 1.2 1.3
2936 45.3 2001 ... 1.6 1.7
2937 46.0 2000 ... 11.0 11.2
[2938 rows x 12 columns]
|
cs |
이제 이 데이터에서 결손값을 제외해야 한다.
|
life.dropna(inplace = True) #dropna()로 결손값 행 삭제
print(life.isnull().sum()) #결손값의 개수를 합한다.
----
Life expectancy 0
Year 0
Alcohol 0
Percentage expenditure 0
Total expenditure 0
Hepatitis B 0
Measles 0
Polio 0
BMI 0
GDP 0
Thinness 1-19 years 0
Thinness 5-9 years 0 #결손값 제거 완료!
|
cs |
dropna() 함수를 이용하면 결손값이 있는 행이나 열을 삭제할 수 있다. 우리는 열 전체 삭제가 아닌 행 전체 삭제를 원하므로 따로 행과 열을 정하는 인자는 지정하지 않았다. 위처럼 dropna로 원본에서 결손값을 삭제하고 결손값의 개수를 세어보면 0으로 없는 것을 확인할 수 있다.
이제 각 변수 사이의 선형 관계를 조사하기 위해 연관 행렬을 생성해보자. 연관 행렬은 판다스 라이브러리의 corr() 함수를 이용하여 생성할 수 있다. seaborn 라이브러리의 hitmap() 함수를 이용하면 시각화까지 할 수 있다.

|
import matplotlib.pyplot as plt
sns.set(rc = {'figure.figsize': (12, 10)})
correlation_matrix = life.corr().round(2) #round2는 소숫점 아래 2까지 나타냄.
sns.heatmap(data = correlation_matrix, annot = True) #seaborn의 히트맵으로 시각화
plt.show()
|
cs |
각 변수 사이의 선형 관계를 히트맵으로 나타내보았다.

숫자들은 상관관계를 보여준다. 이전에도 상관관계에 대해 배운 적이 있는데, 다시 설명하자면 양수인 경에는 양의 상관관계, 즉 정비례이고, 음수는 음의 상관관계를 갖는 것, 즉 반비례이고, 0에 가까울수록 상관관계가 떨어진다. 여기서 -0.45와 -0.46은 Thinness 1-19 years와 Thinness 5-9 years인데, 상호 연관도가 0.93이므로 둘 중에 하나만 사용해도 좋은 중ㅂ고 데이터라 할 수 있다.
상관 관계를 찾고 선형회귀로 나타내자!
그래서 결국 기대수명에 영향을 주는 요소에는 무엇이 있는 걸까?
아래와 같이 'Life expectancy', 'Alcohol', 'Percentage expenditure', 'Measles', 'Polio', 'BMI', 'GDP', 'Thinness 1-19 years' 데이터를 이용해서 쌍 그림(Pair Plot)을 그려 보자.

|
sns.pairplot(life [['Life expectancy', 'Alcohol', 'Percentage expenditure',
'Measles', 'Polio', 'BMI', 'GDP', 'Thinness 1-19 years']])
plt.show()
|
cs |
위의 산포도 그래프를 살펴보면 BMI와 GDP 같은 데이터가 상당한 연관도를 갖는다. 그러면 이제는 이 조사를 바탕으로 알코올 소비량, 보건 예산, 소아마비 접종률, BMI, GDP, 저체중 정봄나을 추출해서 선형회귀를 그려보자.
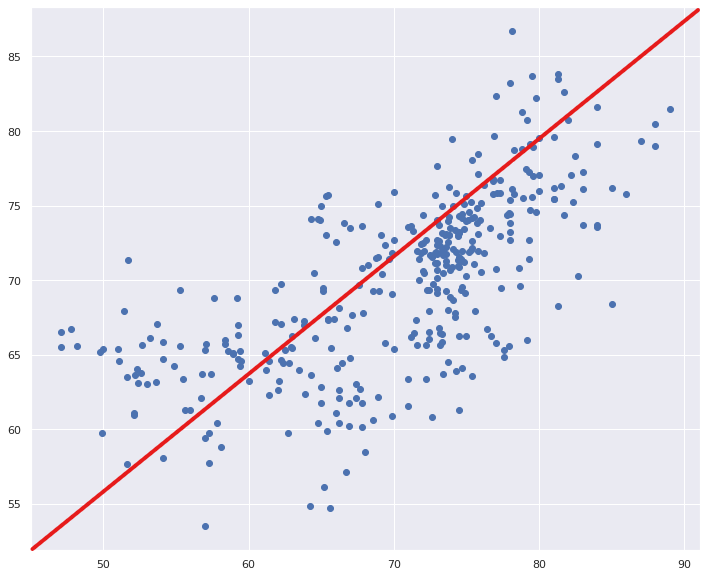
|
X = life[ ['Alcohol', 'Percentage expenditure', 'Polio',
'BMI', 'GDP', 'Thinness 1-19 years']] #학습용 데이터
y = life['Life expectancy'] #학습용 데이터의 정답
#데이터를 80:20으로 분리
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
from sklearn.linear_model import LinearRegression #선형회귀
from sklearn.metrics import mean_squared_error #평균제곱근오차
import numpy as np
lin_model = LinearRegression()
lin_model.fit(X_train, y_train) #선형회귀 모델 생성
y_test_predict = lin_model.predict(X_test) #새 데이터에 대한 예측값
#평균제곱근 오차를 구한다.
rmse = np.sqrt(mean_squared_error(y_test, y_test_predict)
# print('RMSE = ', rmse) # RMSE = 6.492045252348338
plt.scatter(y_test, y_test_predict) #산포도 그래프를 그림.
plt.show()
|
cs |
이 모델에서 평균제곱근 오차는 6.492045252348338로 계산된다. 평균제곱근 오차(Root Mean Squared Error)는 평균제곱오차에 제곱근을 씌워 평균 오차값게 가깝도록 보정한 값이다.
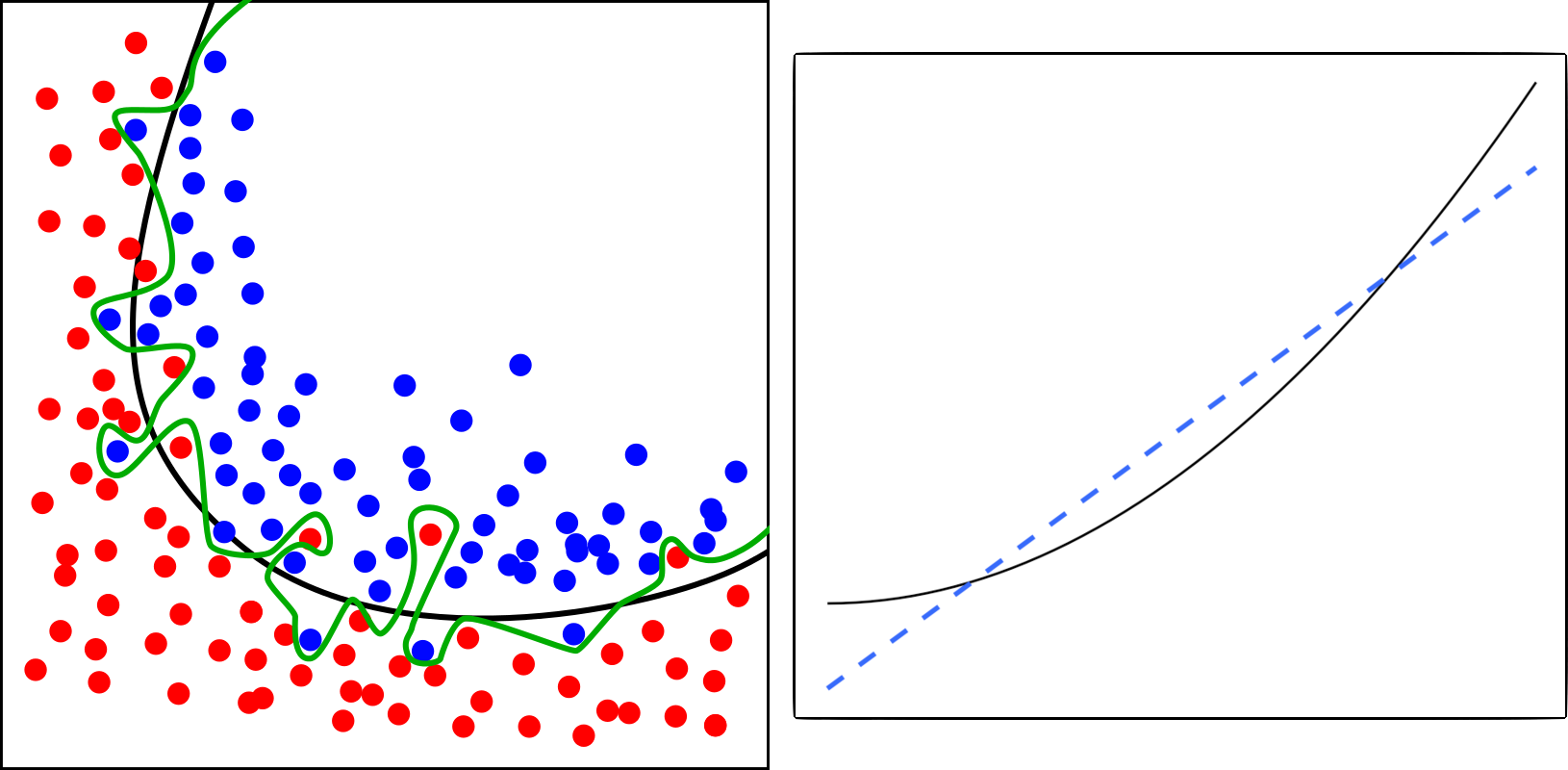
이런 기계학습에서 흔히 볼 수 있는 가능성은 과적합(Overfitting)과 과소적합(Underfitting)이다. 과적합은 학습하는 데이터에서는 성능이 뛰어나지만 새로운 데이터에 대해서는 성능이 잘 나오지 않는 모델을 말하고, 이와 반대로 데이터에 대한 학습이 지나치게 대충 이루어져서 학습 데이터나 다른 새로운 데이터 모두에 대해 예측을 제대로 하지 못하는 모델을 과소적합이라 한다.
위의 그림에서 왼쪽 그림은 데이터의 분포와 이를 설명하는 선이 너무 지나치게 맞춰져 있어서 새로운 데이터의 예측이 떨어지는 편이고, 오른쪽 그림은 데이터의 분포와 이 분포를 설명하는 선이 실제 데이터와 너무 큰 차이를 보인다.
이런 과적합과 과소적합을 막으려면 학습 모델의 복잡도를 높이는 방법으로 해결할 수 있다. 더 많은 데이터를 제공하여 학습을 하는 것이다. 또는 정칙화(Regularization) 기법을 이용할 수도 있다. 수학적으로는 티코노프(Tikhonov) 정칙화라 하고, 통계학에서는 능형 회귀(Ridge Regression), 딥러닝에서는 L2 정칙화라고 부른다.
마무리
이번 시간에는 기계학습의 세 종류 중에서도 지도학습의 회귀분석과 분류에 대해 알아보았다.
마지막으로 심화문제 14.1과 14.3-1), 3-2)를 풀어보고 마치도록 하자. 접은글 속 해답 코드는 참고만 하도록 하자.
14.1: 다음은 P 자동차 회사의 차종과 마력, 그리고 평균 연비(단위: km/l)를 나타내는 표이다.
| A | B | C | D | E | F | G | |
| 마력 | 130 | 250 | 190 | 300 | 210 | 220 | 170 |
| 연비 | 16.3 | 10.2 | 11.1 | 7.1 | 12.1 | 13.2 | 14.2 |
1) 자동차 회사의 마력과 연비 사이에는 어떤 상관관계가 있을까? 선형회귀 분석을 통해서 선혛ㅇ회귀 모델의 절편과 계쑤를 구하여라. 마지막으로 이 선형회귀 모델이 입력 마력 값에 대해 연비를 예측하는 데 얼마나 적합한지 예측 점수를 출력해 보자.
|
계수: [-0.05027473]
절편: 22.58626373626374
예측 점수: 0.8706727649378526
|
cs |
|
from sklearn import linear_model
regr = linear_model.LinearRegression()
horse_power = [ [130], [250], [190], [300], [210], [220], [170] ]
efficiency = [16.3, 10.2, 11.1, 7.1, 12.1, 13.2, 14.2]
regr.fit(horse_power, efficiency)
print('계수: ', regr.coef_)
print('절편: ', regr.intercept_)
print('예측 점수: ', regr.score(horse_power, efficiency))
|
cs |
2) 위의 선형회귀 모델을 바탕으로 270 마력의 신형엔진을 가진 자동차를 개발하려 한다. 이 자동차의 연비를 선형회귀모델에 적용하여 다음과 같이 구해 보자. 출력은 다음과 같이 소수점 둘째 자리까지 출력해 보자.
|
270 마력 자동차의 예상 연비 : 9.01 km/l
|
cs |
|
#1) 문제의 해답 코드
predict = regr.predict([[270]])
print('270 마력 자동차의 예상 연비 : {0:.2f} km/l'.format( predict[0] ) )
|
cs |
14.3: 다음은 철수네 동물병원에 치료를 받은 개의 종류와 그 크기 데이터이다. 이 데이터를 바탕으로 k-NN 알고리즘을 적용해 보자.
- 닥스훈트
| 길이 | 77 | 78 | 85 | 83 | 73 | 77 | 73 | 80 |
| 높이 | 25 | 28 | 19 | 30 | 21 | 22 | 17 | 35 |
- 사모예드
| 길이 | 75 | 77 | 86 | 86 | 79 | 83 | 83 | 88 |
| 높이 | 56 | 57 | 50 | 53 | 60 | 53 | 49 | 61 |
- 말티즈
| 길이 | 34 | 38 | 38 | 411 | 30 | 37 | 41 | 35 |
| 높이 | 22 | 25 | 19 | 30 | 21 | 24 | 28 | 18 |
1) 위의 정보를 바탕으로 닥스훈트를 0, 사모예드를 1, 말티즈를 2로 레이블링하여 데이터와 레이블을 각각 생성하도록 하여라.
|
dog data
[[77 25]
[78 28]
[85 19]
[83 30]
[73 21]
...
[30 21]
[37 24]
[41 28]
[35 18]]
labels
[0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2]
|
cs |
|
import pandas as pd
import numpy as np
dog_data = np.array([[77, 25], [78, 28], [85, 19], [83, 30], [73, 21], [77, 22], [73, 17], [80, 35],
[75, 56], [77, 57], [86, 50], [86, 53], [79, 60], [83, 53], [83, 49], [88, 61],
[34, 22], [38, 25], [38, 19], [41, 30], [30, 21], [37, 24], [41, 28], [35, 18]])
dog_target = []
labels = []
for i in range(len(dog_data)) :
if i <= 7: #1번째~8번째 데이터는 Dachshund, 0번
dog_target.append('Dachshund')
labels.append(0)
elif 8<= i <= 15 : #9번째~16번째 데이터는 Samoyed, 1번
dog_target.append('Samoyed')
labels.append(1)
else : #나머지 데이터는 Maltese, 2번
dog_target.append('Maltese')
labels.append(2)
dog_target = np.array([dog_target]) #넘파이배열화
labels = np.array(labels)
print('dog data \n', dog_data,'\n\n labels \n', labels)
#labels #0: 닥스훈트 1:사모예드 2:말티즈
|
cs |
2) 다음과 같은 데이터 A, B, C, D에 대하여 각각 n_neighbor를 1, 2, 3, 4, 5로 하여 분류하여라.
|
A : 길이 45, 높이 34
B : 길이 70, 높이 59
C: 길이 49, 높이 30
D: 길이 60, 높이 56
|
cs |
|
n_neighbors가 1일 때 분류(A, B, C, D): Maltese Samoyed Maltese Samoyed
n_neighbors가 2일 때 분류(A, B, C, D): Maltese Samoyed Maltese Samoyed
n_neighbors가 3일 때 분류(A, B, C, D): Maltese Samoyed Maltese Samoyed
n_neighbors가 4일 때 분류(A, B, C, D): Maltese Samoyed Maltese Samoyed
n_neighbors가 5일 때 분류(A, B, C, D): Maltese Samoyed Maltese Samoyed
|
cs |
|
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
classes = {0:'Dachshund', 1:'Samoyed', 2:'Maltese'} #레이블과 이름을 매치
X = [[45, 34], [70, 59], [49, 30], [60, 56]] #새 데이터 A, B, C, D
y = knn.predict(X)
for t in [1, 2, 3, 4, 5] :
knn = KNeighborsClassifier(n_neighbors = t) # k=1, 2, 3, 4, 5를 반복
knn.fit(dog_data, labels)
print('n_neighbors가 {0:d}일 때 분류(A, B, C, D): '.format(t), end = "")
for i in range(len(X)) :
print(classes[y[i]], end = " ") #분류한 값을 A, B, C, D 순으로 출력
print("") #줄바꿈
|
cs |
'따라하며 배우는 파이썬과 데이터 과학 > PART 2. 데이터 과학과 인공지능' 카테고리의 다른 글
| Chapter 15. 텐서플로우로 딥러닝의 맛을 보자 (0) | 2021.06.19 |
|---|---|
| Chapter 13. 시각 정보를 다루어보자 (0) | 2021.06.18 |
| Chapter 12. 판다스로 데이터를 분석해보자 (0) | 2021.06.17 |
| Chapter 11. 차트를 멋지게 그려보자 (0) | 2021.06.15 |
| Chapter 10. 넘파이로 수치 데이터를 처리해보자 (1) | 2021.06.15 |