
이번 시간의 목차
1. 데이터 시각화가 꼭 필요할까?
2. 파이썬에서 데이터 시각화의 기본이 되는 맷플롯립
3. plot() 함수를 좀 더 다양하게 써 보자!
4. 막대 그래프를 그려 보자!
5. 산포도 그래프를 그려 보자!
6. 파이 차트를 그려 보자!
7. 히스토그램을 그려 보자!
8. 상자 차트가 뭐지?
9. 한 화면에 여러 좌표평면을 그리려면?
10. 마무리
자, 가자! 파이썬의 세계로!
데이터 시각화가 꼭 필요할까?
우리는 실생활에서 수치 데이터보다는 그림으로 된 데이터를 자주 접한다. 데이터 시각화(Data Visualization)는 시각적 이미지를 사용하여 데이터를 화면에 표시하는 것으로, 점이나 선, 막대그래프 등이 이에 해당한다. 사람들은 시각적으로 보이는 데이터를 직관적으로 이해하기 때문에 데이터 분석에 있어서 데이터 시각화는 빼놓을 수 없는 중요한 기능이다.
데이터 시각화를 사용하는 이유는 크게 두 가지로 나눌 수 있다.
- 사람은 시각화된 정보를 통해 데이터의 비교 분석이나 인과 관계 이해를 더 쉽게 할 수 있다. 데이터 시각화는 인간이 통찰을 통해 데이터에 내재하는 패턴을 알아내는 데도 유용하다.
- 데이터 시각화는 교육이나 홍보 등의 분야에서도 중요한 의사 소통의 도구로간주된다.
너무 어렵게 생각할 것은 없다. 아래의 표와 그래프를 같이 살펴보자.

사람들이 어느 영화를 좋아하는지 위의 표보다 아래의 막대그래프에서 더 빠르게 이해할 수 있다.
잘 만들어진 시각화의 예시를 하나 살펴보자. 아래는 Our World in Data에서 제공하는 코로나-19 바이러스로 인한 사망률을 나타낸 것이다.

https://ourworldindata.org/covid-deaths
Coronavirus (COVID-19) Deaths - Statistics and Research
This page has a large number of charts on the pandemic. In the box below you can select any country you are interested in – or several, if you want to compare countries.
ourworldindata.org
위의 링크를 통해 들어가면 지도형 데이터가 아닌 다양한 그래프로도 나타내어 보여준다.
지도형 그래프에서는 색의 농도에 따라 사망률을 나타내고 있다. 단위는 100으로, 0에서 0.01 사이라면 연한 살구색으로, 20명을 넘어가면 진한 붉은색으로 나타낸다. 이런 우수한 시각화 기법은 복잡한 설명이 없어도 신속하고 효과적인 정보 전달이 가능하고, 빠른 통찰을 이끌어낸다.
파이썬에서 데이터 시각화의 기본이 되는 맷플롯립
파이썬에는 데이터를 시각화하기 위한 많은 도구가 있지만, 그 중에서도 주로 사용하는 것이 맷플롯립(Matplotlib) 라이브러리다. 간단한 막대 그래프, 선 그래프, 산포도를 그리는 용도로서 제격이라고 할 수 있다. 이번 시간에는 matplotlib을 이용해서 다양한 종류의 차트를 만들어 볼 것이다.
|
import matplotlib.pyplot as plt #맷플롯립의 pyplot 모듈
#우리나라의 연간 1인당 국민소득을 각각 years, gdp에 저장
years = [1950, 1960, 1970, 1980, 1990, 2000, 2010]
gdp = [67.0, 80.0, 257.0, 1686.0, 6505, 11865.3, 22105.3]
#선 그래프를 그린다. x축에는 years값, y축에는 gdp값을 표시한다.
plt.plot(years, gdp, color = 'green', marker = 'o', linestyle = 'solid')
#제목을 설정한다.
plt.title('GDP per capita') #1인당 국민소득
#y축에 레이블을 붙인다.
plt.ylabel('dollars')
plt.savefig('gdp_per_capita.png', dpi = 600)
plt.show()
|
cs |
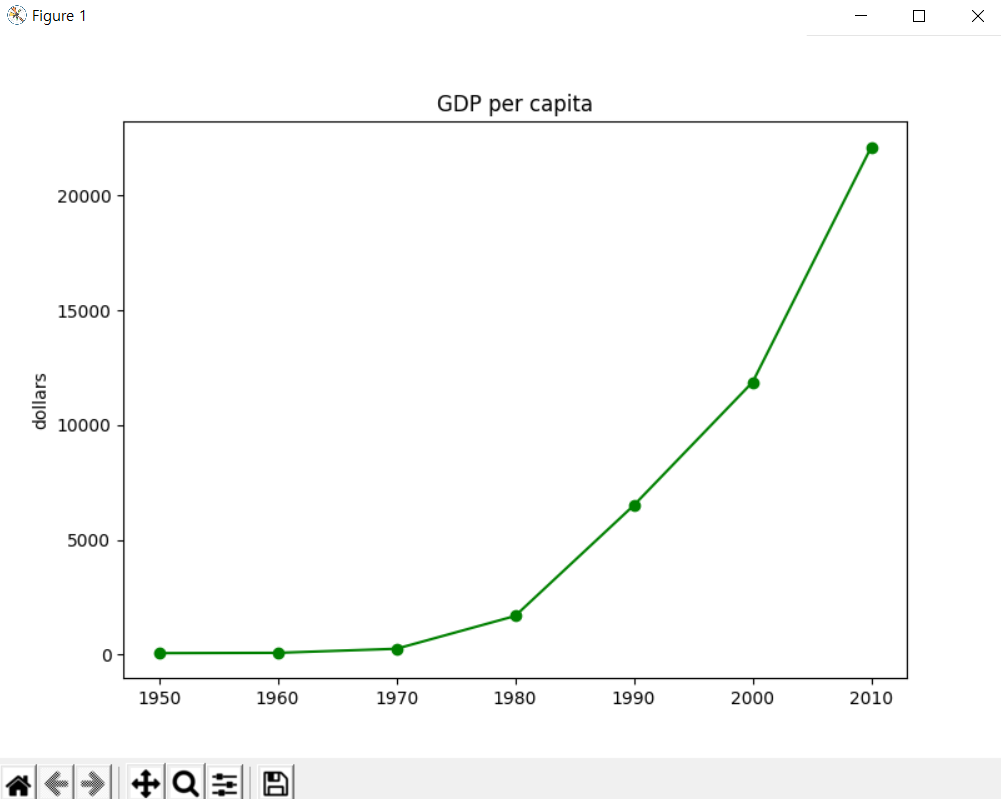
간단하게 맷플롯립의 함수로 연도 별 gdp에 대한 그래프를 그려보았다. 데이터를 어떻게 활용할 것이고, 어떠한 모습으로 그릴지 지정하는 것이 plot() 함수이다.
이제 이 코드를 한 줄씩 살펴보자.
|
import matplotlib.pyplot as plt
|
cs |
먼저 matplotlib 패키지에서 pyplot이라는 서브 패키지(모듈)을 불러온다. import를 시킬 때 뒤에 as 를 붙이면 뒤에 오는 이름을 별명으로 붙여준다. 위의 코드는 pyplot 모듈을 plt로 부르겠다는 뜻이다.
|
years = [1950, 1960, 1970, 1980, 1990, 2000, 2010]
gdp = [67.0, 80.0, 257.0, 1686.0, 6505, 11865.3, 22105.3]
|
cs |
이제 차트를 그릴 데이터가 필요하다. 파일에 저장된 데이터를 읽어 그릴 수도 있지만, 이번에는 간단하게 그려볼 것이니 직접 리스트 형태로 데이터를 입력했다. 그리려는 데이터가 연도별 GDP의 변화이기 때문에 years와 GDP라는 리스트를 생성한다.
|
plt.plot(years, gdp, color = 'green', marker = 'o', linestyle = 'solid')
# x축이 years, y축이 gdp
# 그래프의 색은 'green', 점은 'o' 로 표시한다.
# 선의 형태는 직선으로 한다.
|
cs |
데이터가 준비됐다면 plot() 함수로 그래프를 그린다. plot() 함수는 x축 데이터와 y축 데이터를 필수 인자로 받고, 위의 선 색깔, 점, 선의 두께나 형태 등을 추가로 설정할 수 있다.
|
plt.title('GDP per capita') #1인당 국민소득
plt.ylabel('dollars')
plt.savefig('gdp_per_capita.png', dpi = 600)
plt.show()
|
cs |
그런 다음 차트의 제목을 'GDP per capita(1인당 국민소득)' 이라고 붙인다. 이때는 title() 함수를 사용한다. 이 제목은 차트의 최상단에 표시된다. ylabel() 함수로 y축에 'dollars'라는 라벨을 붙여주고, savefig() 함수를 통해 차트 이미지를 저장한다. 이때 dpi는 해상도를 의미한다. 그리고 마지막으로 show()함수를 써 준다. 이 show() 함수는 화면에 차트를 표시하는데, 이 함수를 써주지 않으면 아무리 코드를 잘 짜 놓아도 실제로 그래프를 확인할 수 없으니 꼭 써야 한다.
마지막으로 실행시키면...

제대로 그래프가 그려진 것을 볼 수 있다.
plot() 함수를 좀 더 다양하게 써 보자!
plot()은 한 화면에 여러 개의 그래프를 그릴 수도 있다. 이번에는 2x, x² + 5, -x² - 5의 세 가지 함수를 그려보자.

2x는 빨간색 긴 점선, x² + 5는 초록색 실선에 세모 점, -x² - 5는 파란색 점선에 별 점을 사용할 것이다.
|
import matplotlib.pyplot as plt
x = [x for x in range(-20, 20)] # -20, 20 사이의 x를 정수 단위로 생성
y1 = [2 * t for t in x] # x에 대해 2x값을 생성한다.
y2 = [t ** 2 + 5 for t in x] # x에 대해 x ** 2 + 5 값을 생성한다.
y3 = [-t ** 2 - 5 for t in x] # x에 대해 -x ** 2 - 5 값을 생성한다.
|
cs |
시작은 항상 import matplotlib.pyplot as plt로 시작한다. (지금부터는 이 문장을 생략하도록 하겠다.)
우선 y값을 만들기 전에 x값부터 있어야 한다. 이 그래프에서는 x의 범위를 -20에서 20까지로 제한한다. 리스트 함축 표현을 사용하면 x값을 쉽게 만들어낼 수 있을 것이다.
그 다음 2x, x² + 5, -x² - 5에 맞는 y값을 만들어낸다. 이 역시도 리스트 함축 표현을 사용하면 빠르게 만들 수 있다.
|
plt.plot(x, y1, color = 'red', linestyle = '--')
plt.plot(x, y2, color = 'green', marker = '^', linestyle = '-')
plt.plot(x, y3, color = 'blue', marker = '*', linestyle = ':')
|
cs |
그 다음 plt( ) 함수로 그래프를 그린다. 이번에 바꿀 설정은 색깔과 선형, 그리고 점 모양이 있다.
여기서 긴 점선은 '--'로, 완전한 점선은 ':', 실선은 '-'로 나타낸다.
그리고 삼각형 점은 '^'로, 별 점은 '*'로 나타낼 수 있다. 이 말고도 다양한 옵션이 존재한다. 자세한 옵션은 아래 이미지를 참고하자. 아래 이미지는 matplotlib.org 에 설명이 더 있다.

https://matplotlib.org/2.0.2/examples/lines_bars_and_markers/line_styles_reference.html

https://matplotlib.org/2.0.2/examples/lines_bars_and_markers/marker_reference.html
이렇게 하나의 차트에 여러 개의 데이터를 중첩해서 그리면 데이터 분석에 도움이 된다. 하지만 그래프가 너무 겹치다 보면 어느 것이 어느 데이터를 나타내는지 알기 어려울 때가 있다.

|
import matplotlib.pyplot as plt
x = [x for x in range(20)] #0에서 20까지의 정수 x
y = [x ** 2 for x in range(20)] #0에서 20까지의 정수 x에 대한 x ** 2
z = [x ** 3 for x in range(20)] #0에서 20까지의 정수 x에 대한 x ** 3
plt.plot(x, x, label = 'linear') #각 선에 대한 레이블(설명)
plt.plot(x, y, label = 'quadratic')
plt.plot(x, z, label = 'qubic')
plt.xlabel('x label') #x축 라벨
plt.ylabel('y label') #y축 라벨
plt.title('Graph') #차트 제목
plt.legend() #디폴트 위치에 범례 생성
plt.show()
|
cs |
위의 그래프에는 어느 그래프가 무슨 데이터를 나타내고 있는지 왼쪽 상단에 보여준다. 방금 전 2x, x² + 5, -x² - 5 그래프를 그린 코드와 지금 코드가 무엇이 다른지 알아볼 수 있겠는가? 바로 legend() 함수이다. 이 legend는 범례로, 이름 그대로 각 그래프에 대한 설명을 간략하게 나타내준다. 이 legend()를 표시하면 그래프끼리 서로 헷갈릴 일도 없다.
막대 그래프를 그려 보자!
pyplot에서는 선으로 된 그래프 뿐만 아니라 막대 그래프, 산포도 그래프, 파이 차트, 히스토그램, 상자 차트 등 다양한 차트를 지원한다. 이번에는 아까 그려본 1인당 국민소득을 막대 그래프로 그려보자.
|
import matplotlib.pyplot as plt
#또는 from matplotlib import pyplot as plt 로 쓸 수도 있다.
#1인당 국민소득
years = [1950, 1960, 1970, 1980, 1990, 2000, 2010]
gdp = [67.0, 80.0, 257.0, 1686.0, 6505, 11865.3, 22105.3]
plt.bar(range(len(years)), gdp) #막대그래프 호출: bar(x, y)
plt.title("GDP per capita") #차트 제목
plt.ylabel('dollars') #y축 라벨
plt.xticks(range(len(years)), years) #x축에 틱을 붙임.
plt.show()
|
cs |

막대 그래프를 그리려면 bar(x, y) 함수를 사용한다. 이때 x로 들어가는 인자는 가로축의 개수가 된다. 위에서는 range(len(years))를 넣어줬으므로 range()의 인자인 len(years), 즉 7을 따라 0에서 6까지의 정수 범위를 만들고, 이를 가로축으로 세운다.
그런데 이때 가로축의 눈금은 0부터 6까지의 정수가 아닌 연도로 설정되어 있다.
이 눈금을 설정하는 함수가 바로 xticks(x, y)함수이다. x인자로 받은 축의 눈금에 y라는 값을 넣어준다. 위에서는 range(len(years))마다 years에 해당하는 값을 붙여주었다.
이 막대형 차트도 한 막대에 여러 데이터에 관한 값이 들어갈 수 있다.
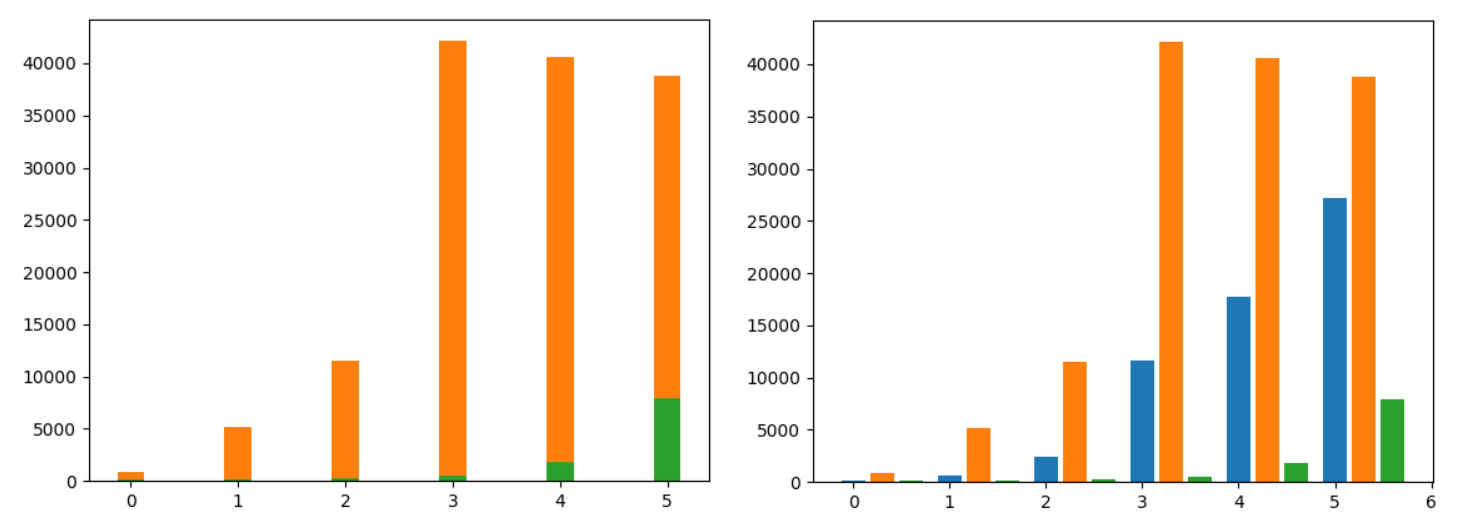
|
import matplotlib.pyplot as plt
#1인당 국민소득
years = [1965, 1975, 1985, 1995, 2005, 2015]
ko = [130, 650, 2450, 11600, 17790, 27250]
jp = [890, 5120, 11500, 42130, 40560, 38780]
ch = [100, 200, 290, 540, 1760, 7940]
#왼쪽 그래프
x_range = range(len(years)) #가로축
plt.bar(x_range, ko, width = 0.25)
plt.bar(x_range, jp, width = 0.25)
plt.bar(x_range, ch, width = 0.25)
plt.show()
#오른쪽 그래프
import numpy as np
x_range = np.arange(len(years)) #가로축
plt.bar(x_range + 0.0, ko, width = 0.25)
plt.bar(x_range + 0.3, jp, width = 0.25)
plt.bar(x_range + 0.6, ch, width = 0.25)
plt.show()
|
cs |
위의 코드에서 width = 0.25는 막대의 두께를 조절한다.
왼쪽 그래프는 그래프가 겹쳐져 있어서 파란색(한국) 그래프는 보이지도 않는다. 따라서 그래프의 위치를 조금 조정해서 각각의 그래프가 잘 보이도록 해야 할 필요가 있다.
그렇게 수정한 코드가 아래의 코드이다. 각 항목에 실수를 바로 더할 수 없는 리스트 대신 넘파이를 불러와서 가로축 x_range를 넘파이 배열로 만든다. 넘파이 배열로 만들어진 목록에 각각 0, 0.3, 0.6을 더하면 그래프가 실수만큼 오른쪽으로 이동한다. 이제 오른쪽으로 조금씩 밀려서 전부 보인다! 비교하기도 좋다.
산포도 그래프를 그려 보자!
이번에는 산포도 그래프를 그려 보자.
산포도 그래프(혹은 플롯, Scatter Plot)은 개별 데이터 포인트를 그리는 차트이다. 선형 그래프와 다른 점이라면 각 지점이 선으로 연결되지 않는다는 것이 있다.
|
import matplotlib.pyplot as plt
import numpy as np
xData = np.arange(20, 50)
yData = xData + 2 * np.random.randn(30) #xData에 randn() 함수로 잡음을 섞는다.
#이 잡음은 정규분포를 따른다.
plt.scatter(xData, yData) #산포도 그래프 호출: scatter(x, y)
plt.title('Real Age vs Physical Age')
plt.xlabel('Real Age')
plt.ylabel('Physical Age')
plt.savefig('age.png', dpi = 600)
plt.show()
|
cs |

이 scatter() 함수의 키워드 인자 중에는 이 점의 불투명도를 조절하는 키워드도 있다. 이는 나중에 도전문제 풀이에서 자세히 다뤄 보자.
파이 차트를 그려 보자!
이번에는 파이 차트를 그려 보자.
파이 차트(Pie Chart)는 데이터의 값에 따라서 원형 비율로 나누어져 있는 차트다. 모양을 떠올리기 어렵다면 초등학교 때 자주 그리던 방학 생활 계획표를 떠올리면 된다. 이번 예시도 생활 계획표를 만드는 것이다.
이 파이 차트는 그냥 원이 있고 원의 영역을 나누기만 한 것이기 때문에 각 항목을 비교하기 어려울 수도 있다. 그래서 일반적으로는 영역의 데이터나 비율 등을 표시하고 쓴다.
|
import matplotlib.pyplot as plt
times = [8, 14, 2] #각각 수면/학습/휴식 시간
plt.pie(times)
plt.show()
|
cs |

파이 차트를 그리는 방법은 간단하다. 우선 pie(x) 함수를 사용한다. 이 x에는 원의 비율을 나누는 데이터가 들어갈 수 있다. 위의 코드에서는 times = [8, 14, 2] 라는 수면, 학습, 휴식 시간에 대한 데이터를 넣어주었다.
하지만 이렇게 끝내면 무슨 영역이 무슨 활동을 가리키는지 알기 어렵다. 그래서 우리는 몇 가지 코드를 더 추가해줘야 한다.
|
import matplotlib.pyplot as plt
times = [8, 14, 2]
timetables = ['Sleep', 'Study', 'Rest'] #각 시간에 하는 활동
#autopct는 백분율을 표시한다. 여기서는 소수점 2번째 자리까지 표시한다.
#labels 매개변수로 timetable 을 준다.
plt.pie(times, autopct = '%.2f', labels = timetables)
plt.show()
|
cs |

timetables 라는 리스트를 새로 만들어 라벨을 붙여주고, autopct 키워드를 통해 백분율까지 나타내줬다. 이렇게 하니 데이터를 좀 더 알기 쉬워졌다!
히스토그램을 그려 보자!
히스토그램(Histogram)은 주어진 자료를 몇 개의 구간으로 나누고 각 구간의 도수(Frequency)를 조사하여 나타낸 막대 그래프이다. 히스토그램은 아주 유용한 시각화 도구로, 이를 통해 자료의 분포 상태를 한눈에 볼 수 있다.
|
import matplotlib.pyplot as plt
#8명이 1년 동안 읽은 책의 권수
books = [1, 6, 2, 3, 1, 2, 0, 2]
plt.hist(books) #히스토그램 호출: hist(x)
plt.xlabel('books')
plt.ylabel('frequency')
plt.show()
|
cs |

히스토그램을 그리려면 hist(x) 함수를 호출한다.
위의 예시에서는 1년 동안 학생 8명이 읽은 책의 권수를 히스토그램으로 나타내보았다. 이 히스토그램의 x축에는 8명이 읽은 권수의 종류가 들어가고, y축에는 권수마다 몇 명이 그만큼 읽었는지가 들어간다.
그런데 이렇게 끝내면 한 가지 문제가 생긴다. 각 막대와 눈금이 맞지 들쭉날쭉한다.
이럴 때 쓰는 것이 빈(Bin)이다. 빈은 x축에 들어간 데이터의 값을 동일한 구간으로 나누어 준다. 위처럼 빈을 따로 설정하지 않으면 10칸으로 나누어진다.
|
plt.hist(books, bins = 6)
|
cs |

빈의 개수를 따로 설정하려면 hist(x, bins = n) 형태로 입력해주면 된다. 막대와 눈금의 간격을 맞추려면 각 데이터의 최댓값 (여기선 가장 책을 많이 읽은 사람이 6권 읽었으므로 6이다.)으로 빈을 설정하면 된다. 위의 코드를 추가했더니 이제 막대와 눈금의 간격이 들어맞는 것을 볼 수 있다.
이 히스토그램도 한 화면에 여러 종류를 그릴 수 있다.
|
import numpy as np
import matplotlib.pyplot as plt
n_bins = 10
x = np.random.randn(1000) #정규분포를 따르는
y = np.random.randn(1000) #무작위 난수 1000개
plt.hist(x, n_bins, histtype = 'bar', color = 'red')
plt.hist(y, n_bins, histtype = 'bar', color = 'blue', alpha = 0.3)
#두 번째 인자는 빈의 개수.
#alpha 키워드는 불투명도를 조절한다.
plt.show()
|
cs |

불투명도를 조절하려면 alpha 키워드 인자를 이용한다. 이 alpha는 불투명도를 0에서 1 사이로 설정할 수 있다. 0과 가까워질수록 투명해지고, 1과 가까워질수록 불투명해진다.
상자 차트가 뭐지?
상자 차트(Box Chart)는 데이터의 최대, 최소, 중간값과 사분위 수 등을 효율적으로 가시화할 수 있는 차트이다. 상위 25%와 하위 25%의 범위를 나타내는 상자가 있고, 데이터의 범위를 표시하는 수염이 있어서 상자-수염(Box-and-Whisker)차트라고도 부른다.
|
import numpy as np
import matplotlib.pyplot as plt
random_data = np.random.randn(100) #무작위 데이터 100개
plt.boxplot(random_data) #상자 차트 호출: boxplot(x)
plt.show()
|
cs |

상자 차트를 그리려면 boxplot(x) 함수를 사용한다.
그래프에서 사각형은 사각형 속 주황색 선이 나타내는 중앙값(Median)을 중심으로 상위 25%와 하위 25%의 값이 모여 있는 구간을 표시한다. 이 사각형의 위와 아래로 뻗은 선은 위스커(Whisker) 혹은 수염이라 부른다. 이 위스커의 끝과 끝까지가 데이터가 분포하는 범위이다.
하지만 그래프를 보면 이 위스커의 범위 밖에 점이 찍힌 것도 있다. 이는 이상치(Outlier)라고 하고, 결국 데이터의 범위를 표시하는 위스커가 데이터 전체를 포함하지 않고 튀는 값은 제외한다는 것이 된다.
그렇다면 위스커의 범위는 무엇을 기준으로 범위를 정하는 것일까?
상다의 윗부분 Q3에서 상자의 밑부분 Q1의 값을 뺀 Q3 - Q1을 사분범위 혹은 IQR(Inter-Quartile Range)라고 한다. 데이터가 상자의 윗부분에서 위로 IQR의 1.5배 이상 올라가면 이상치로 간주하고, 하단에서도 마찬가지로 1.5배 이상 낮아지면 이상치로 분류하게 된다. 위스커는 이런 이상치를 제외하고 남은 데이터의 최댓값과 최솟값을 표시한다.
늘 그렇듯 이 상자 차트도 한 화면에 여러 상자를 그릴 수 있다.
|
import numpy as np
import matplotlib.pyplot as plt
data1 = [1, 2, 3, 4, 5]
data2 = [2, 3, 4, 5, 6]
plt.boxplot([data1, data2]) #왼쪽 그래프
plt.boxplot(np.array([data1, data2])) #오른쪽 그래프
plt.show()
|
cs |
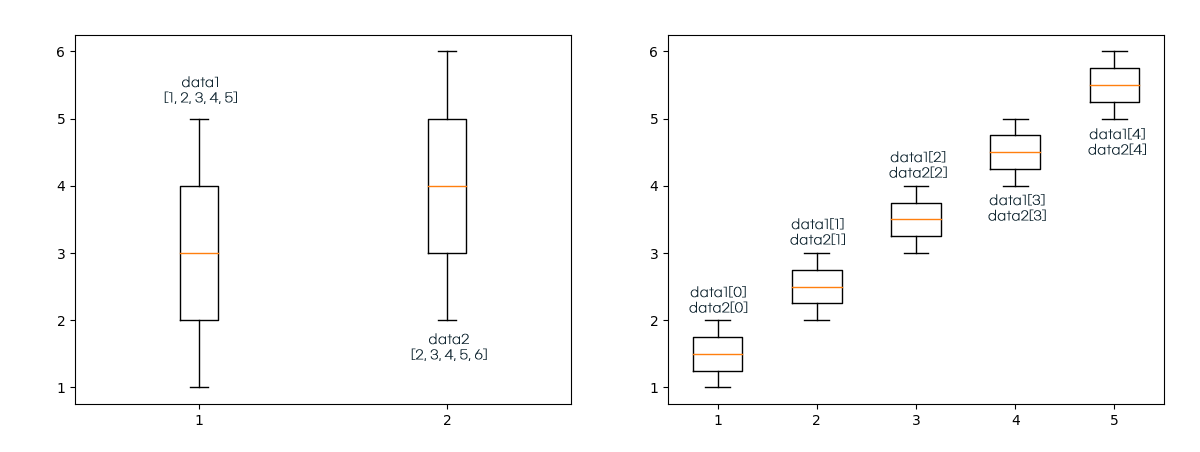
상자 차트는 기존 리스트로 묶어 데이터를 줄 때와 넘파이 배열로 묶어 데이터를 줄 때의 결과가 다르다. 리스트로 넘겨주면 리스트 각각의 단위로 처리하지만, 넘파이 배열로 넘겨주면 열 단위로 끊어 그래프를 그린다.
한 화면에 여러 좌표평면을 그리려면?
우리는 이때까지 한 좌표평면에 여러 그래프는 그려 봤지만 한 화면에 여러 좌표평면, 각각의 그래프를 그려본 적은 없다. pyplot에서는 한 화면에 여러 그래프를 나눠 그리는 함수를 제공한다. 바로 subplots(x, y) 함수이다. x에는 행의 개수, y에는 열의 개수가 들어간다.
|
import matplotlib.pyplot as plt
import random
# 2 * 2 개의 그래프, 5 * 5인치 크기 화면
fig, ax = plt.subplots(2, 2, figsize = (5, 5))
ax[0, 0].plot(range(10), 'r') #row 0, col 0 (0행 0열)
ax[1, 0].plot(range(10), 'b') #row 1, col 0
ax[0, 1].plot(range(10), 'g') #row 0, col 1
ax[1, 1].plot(range(10), 'k') #row 1, col 1
plt.show()
|
cs |

이때 ax[n1, n2]는 그래프를 그릴 공간을 택한다. 이렇게 한 번에 그리는 방법 말고, 도식을 먼저 생성한 뒤에 도식에다 서브플롯을 추가하는 add_subplot() 함수를 쓸 수도 있다.
|
fig = plt.figure()
ax1 = fig.add_subplot(2, 2, 1)
ax2 = fig.add_subplot(2, 2, 2)
ax3 = fig.add_subplot(2, 2, 3)
ax4 = fig.add_subplot(2, 2, 4)
plt.show()
|
cs |

add_subplot() 함수의 첫 인자는 그려지는 서브플롯의 행, 두 번째 인자는 열의 수를 나타내므로 위의 코드는 2행 2열짜리 서브 플롯을 만든다. 마지막 인자는 생성되는 서브플롯의 인덱스로, 0으로 시작하는 리스트나 튜플, 넘파이배열 등과는 달리 1부터 시작한다.
마무리
이번 시간에는 데이터를 시각화하는 여러 방법에 대해 알아보았다.
마지막으로 도전문제 11.1, 11.4, 심화문제 11.2, 11.4를 풀어보고 마치도록 하자. 접은글 속 해답코드는 참고만 하도록 하자.
도전문제
11.1 : 넘파이의 난수 생서을 이용하여 1000개의 난수를 생성하고 생성된 순서대로 화면에 다음과 같이 그리는 일을 해 보라. 가로축은 생성된 순서, 세로축은 생성된 값이 될 것이다.

|
import matplotlib.pyplot as plt
import numpy as np
x = [x for x in range(1000)] #순서는 0부터 1000까지의 정수.
y = [y * 6 - 3.0 for y in np.random.rand(1000)] #최대 3, 최소 -3의 데이터를 만든다.
plt.plot(x, y, marker = 'o')
plt.axis([-5, 1005, -3, 3]) #그래프가 그려질 영역. (x1, x2, y1, y2)
plt.title('numbers') #제목을 numbers 로 설정.
plt.show()
|
cs |
11.4 : 난수를 발생시켜 임의의 2차원 좌표를 생성해 그려보자. 이때 좌표의 x와 y값은 표준정규분포를 따르도록 할 것이다. 그러면 생성된 좌표는 원점 (0, 0)에 밀집한 모양을 가질 것이다. scatter() 함수 내에 불투명도를 의미하는 alpha 키워드 매개변수에 1보다 작은 값을 주어 점이 많이 겹칠 때 더 진하게 보이게 만들 수 있다.

|
import matplotlib.pyplot as plt
import numpy as np
xData = [x for x in np.random.randn(10000)] #10000개의 무작위 난수
yData = [y for y in np.random.randn(10000)] #10000개의 무작위 난수
plt.scatter(xData, yData, alpha = 0.1) #alpha = 0.02 : 왼쪽 alpha = 0.1 : 오른쪽
plt.title('Random Position')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
|
cs |
심화문제
11.2 : 넘파이의 sin(), cos() 함수를 호출하여 그림과 같은 주기함수를 표현해 보자. sin(), cos() 등의 삼각함수는 그 주기가 2π이므로 (2 * np.pi) * 6을 통해 6번 반복되는 주기함수를 얻을 수 있다. 이 코드에서 sin() 함수는 빨간색 실선으로 표시되는데, x값이 커질수록 y의 진폭이 커지도록 하여라. cos() 함수는 파란색 점선으로 나타나 있는데, 출력값은 -1에서 1사이이므로 이 값에 20을 곱하여 -20에서 20사이의 진폭을 가지도록 하여라.

|
import matplotlib.pyplot as plt
import numpy as np
a = np.arange(0, (2 * np.pi) * 6 + 2, 0.1) #6번 반복 / 0.1 간격으로 x 생성
plt.plot(a, a * np.sin(a), color = 'red') # a가 증가하므로 sin(a)에 a를 곱하면 증가한다.
plt.plot(a, 20 * np.cos(a), '--', color = 'blue') #진폭 20
plt.show()
|
cs |
11.4 : numpy의 난수생성기를 이용하여 각각 1000개의 난수를 가지는 3가지 종류의 (x, y) 분포를 생성하고 matplotlib의 산포도 그래프로 나타내어라. 왼쪽의 그림은 x값과 y값이 각각 평균이 25이고 표준편차가 6인 특성을 가진다. 가운데 그림은 x값 평균이 25이고 표준편차가 6인 특성을 가지며, y값은 평균이 25이고 표준편차가 3인 특성을 가진다. 가장 오른쪽은 x 값의 평균이 25이고 표준편차가 6인 특성을 가지며 y갑승ㄴ x값에 표준정규분포 난수를 더한 값이다.

|
import matplotlib.pyplot as plt
import numpy as np
mu = 25 #평균은 전부 25이다.
sigma1 = 6 #표준편차1
sigma2 = 3 #표준편차2
#정규분포 = 평균 + 표준편차 * 수
x = [mu + sigma1 * np.random.randn(1000)]
y1 = [mu + sigma1 * np.random.randn(1000)]
y2 = [mu + sigma2 * np.random.randn(1000)]
y3 = [x + np.random.rand(1000)]
#서브플롯으로 나타낸다. (행이 1, 열이 3)
fig, ax = plt.subplots(1, 3)
ax[0].scatter(x, y1)
ax[1].scatter(x, y2, color = 'red')
ax[2].scatter(x, y3, color = 'green')
plt.show()
|
cs |
'따라하며 배우는 파이썬과 데이터 과학 > PART 2. 데이터 과학과 인공지능' 카테고리의 다른 글
| Chapter 14. 기계학습으로 똑똑한 컴퓨터를 만들자 (0) | 2021.06.19 |
|---|---|
| Chapter 13. 시각 정보를 다루어보자 (0) | 2021.06.18 |
| Chapter 12. 판다스로 데이터를 분석해보자 (0) | 2021.06.17 |
| Chapter 10. 넘파이로 수치 데이터를 처리해보자 (1) | 2021.06.15 |
| Chapter 09. 텍스트를 처리해보자 (0) | 2021.06.14 |